КОМЕДИЯ ОШИБОК

КОМЕДИЯ ОШИБОК

Бекман родился в Миддельбурге, главном городе нидерландской провинции Зеландия. В 1607 – 1610 годах изучал теологию в Лейдене, одновременно зарабатывая себе на жизнь изготовлением свечей и прокладкой водопроводных труб. В 1618 году он окончил университет в Кане (Caen) со степенью доктора медицины, но врачом не стал и зарабатывал на жизнь преподаванием в школах Утрехта, Роттердама и Дордрехта. В Бреду он приехал, чтобы помочь своему дяде в забое свиней, а заодно и подыскать себе невесту.

Как-то, скорее всего в ноябре – декабре 1618 года, более точную дату установить уже невозможно, Бекман задал Декарту вопрос, касавшийся свободного падения тел. Декарт набросал ответ, который Бекман сохранил и спустя десять лет записал в свой дневник (Journal)1476, истолковав картезианское решение так, как он его понял. По словам Александра Койре, Декартовы рассуждения представляли собой смесь «математического изящества с самой безнадежной физической путаницей»1477.

Рис. 3.1. К рассуждениям Декарта о величине угла

Бекмана интересовал следующий вопрос1478: «Можем ли мы, исходя из принятых мною начал, а именно: в вакууме тело, некогда приведенное в движение, будет всегда пребывать в движении; между Землей и падающим камнем находится вакуум, – определить, какое расстояние прошло [падающее] тело за час, если известно, какой путь оно прошло за два часа?»1479

Декарт начинает свой ответ с утверждения, что «сила движения (force de se mouvoir)» падающего тела возрастает пропорционально длине поперечных линий de, fg, hi и т.д. [рис. 3.2]1480. На этой диаграмме в соответствии с позднесредневековой традицией по вертикали (или, как тогда говорили, «по широте») «откладывается» время, то есть экстенсионал движения от точки a к точке b (то есть от начальной к конечной точке пути)1481, а по горизонтали («по долготе») – интенсионал, или степень движения (Декарт использовал выражение «сила движения»1482, что в нашем понимании примерно соответствует скорости или кинетической энергии движения; скажем, к моменту h скорость падающего тела достигла величины hi). Тогда площадь прямоугольника fhio будет представлять то движение, которое тело приобрело за интервал времени fh.

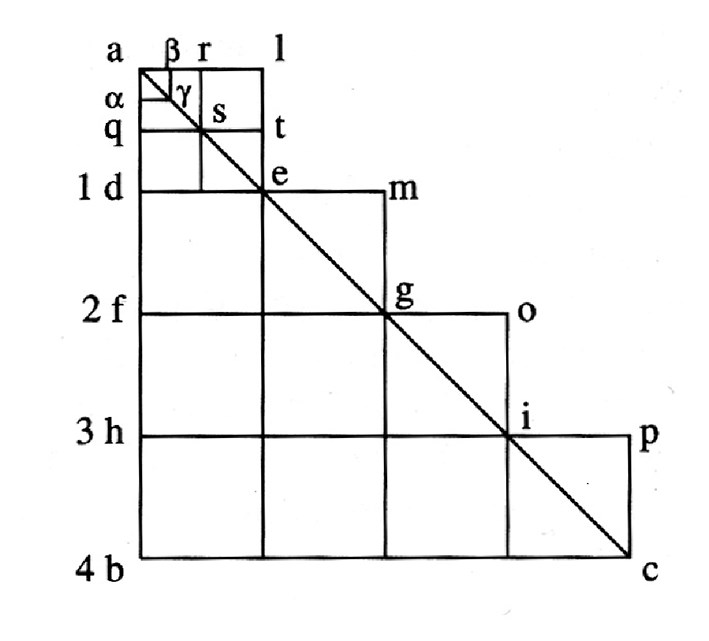
Рис. 3.2. К картезианскому определению возрастания «силы движения» под действием притяжения Земли (1618)

Итак, Декарт определяет величину возрастания «силы движения» под действием «притяжения Земли» в предположении, что это возрастание происходит дискретно:

я принимаю в качестве первого минимума… движения1483, обусловленного первой, которую можно представить, силой притяжения Земли, квадрат aled (то есть величина возрастания интенсивности движения падающего тела за первый промежуток времени может быть геометрически представлена квадратом aled. – И.Д.). Для второго минимума движения получаем удвоенный [квадрат], то есть dmgf; способность (force) движения, которая имелась в первом минимуме, сохраняется и к ней добавляется новая, равная ей способность (то есть за следующий промежуток времени интенсивность движения возрастает на ту же величину. – И.Д.). В третий минимум движения будет [действовать] утроенная способность… и т.д..

Таким образом, свободное падение геометрически может быть представлено треугольником abc.

Если перевести рассуждения Декарта на современный язык (хотя такими «переводами» следует пользоваться с большой осторожностью), то можно сказать, что за равные промежутки времени ?t₁, ?t₂, ?t₃ и т.д. скорость падения возрастает на одну и ту же величину, то есть движение является равноускоренным: v = at.

Но, – продолжает Декарт, – вы мне скажете, что есть части ale, emg, goi и т.д., которые выступают за этот треугольник (то есть за линию ac. – И.Д.), и потому треугольник не может объяснить эту прогрессию (то есть равномерное возрастание интенсивности движения (скорости, в современной терминологии). – И.Д.). Однако я отвечу, что эти выступающие части образуются оттого, что мы приписали широту минимуму, который должен представляться неделимым и не состоящим из частей (то есть вертикаль ab, которая отображает время падения, представлена состоящей из одинаковых дискретных частей – ad, df и т.д., тогда как в действительности время течет непрерывно, а не скачками. – И.Д.).

Далее Декарт делит «минимум» ad и сторону al пополам, получая четыре меньших квадрата (arqs и др.), тогда первым «минимумом движения» станет arqs, а вторым – qtde (который вдвое больше «первого минимума» arqs), при этом сторона qt будет представлять «удвоенный минимум способности» движения. После этого выступающими частями станут меньшие треугольники ars, ste. Затем Декарт аналогичным образом поступает с квадратом arqs, получая еще меньший квадрат a??? и т.д. После этого такие же операции деления проделываются со сторонами df, fh и т.д. В результате подобного деления отрезков выступающие треугольники становятся все меньше и меньше, и в итоге мы придем, как выразился Декарт, к «истинному минимуму, то есть к точке, и тогда уже не будет никаких выступающих частей». Таким образом, если перейти к непрерывно текущему времени (и, соответственно, к непрерывно возрастающей «силе движения»), то количество движения будет представлено треугольником abc.

Прежде всего следует отметить, что Декарт вовсе не доказывает, что свободное падение представляет собой равноускоренное движение, но лишь иллюстрирует это обстоятельство графически.

Кроме того, Декарт подчеркивает, что Бог в каждый момент времени создает силу притяжения, действующую на падающее тело, и постулат Бекмана о сохранении движения в вакууме он интерпретирует следующим образом: после того как Бог в первый момент падения камня создал в нем некую силу притяжения, дальнейшее движение камня в пустоте поддерживается той же силой, точнее, в каждый последующий момент Бог создает в камне ту же силу, какую Он создал в начальный момент.

Формулируя выводы из приведенного рассмотрения, Декарт утверждает, используя в качестве иллюстрации геометрическое постороение, приведенное на [рис. 3.3] (где ag = gb и af = fc), что площадь треугольника agf относится к площади трапеции gfbc (а следовательно, и соответствующие количества движения) как 1: 3 (что нетрудно доказать), откуда следует, что «часть gb, которая есть половина [ab], будет проходиться камнем в три раза быстрее, чем другая половина ag».

Рис. 3.3. К картезианскому анализу свободного падения (1618)

Но ведь до этого Декарт под экстенсионалом движения имел в виду не путь, но время! Почему же он, формулируя вывод, меняет смысл экстенсионала? Основанием для замены временного экстенсионала пространственным стало одно из принятых (еще Аристотелем) толкований скорости: быстрее, то есть с большей скоростью, движется то тело, которое за одно и то же время пройдет больший путь, или в формульной записи: при ?t₁=?t₂ V₁/V₂ = S₁/S₂. Таким образом, можно допустить, что Декарт совершенно правильно полагал, что если за первый час тело прошло расстояние S, то за второй час оно пройдет путь 3S, или, иными словами, если за час тело проходит расстояние S, то за два часа – 4S, то есть S ~ t². Именно так вывод Декарта понял Бекман. Однако цитированные выше слова из заключительного абзаца декартовского анализа можно (если исходить из буквального понимания текста) толковать иначе: вторую половину пути падающее тело проходит с втрое большей скоростью, чем первую, что, разумеется, неверно.

Обратимся теперь еще к одному документу 1618 года – дневниковой записи Декарта, где он вкратце излагает свое решение задачи, предложенной Бекманом. Запись сделана вскоре после написания рассмотренного выше документа (возможно, что этот документ уже был отослан Бекману и дневниковую запись Декарт делал по памяти). Вот как он истолковал в дневнике вопрос Бекмана и свой ответ на него:

Камень, как он (то есть Бекман. – И.Д.) сказал, падает из точки A в точку B в течение часа [рис. 3.4]. Камень при этом постоянно притягивается Землей с одной и той же силой, не теряя скорости, запечатленной в нем предыдущим притяжением. По его [Бекмана] мнению, то, что движется в вакууме, будет двигаться всегда. Его вопрос: за какое время камень пройдет этот путь (то есть AD. – И.Д.)?

Как видим, в дневниковой записи вопрос Бекмана представлен в несколько иной формулировке, чем в первоначальном документе. Это неудивительно, поскольку задача Декартом уже была решена, и потому он переформулировал вопрос в более общем виде. Но – и это самое главное – Декарт в дневнике дает на поставленный вопрос (неважно, какой именно, ибо как бы вопрос ни формулировался, речь фактически шла о зависимости пути от времени при равноускоренном движении) совершенно иной ответ:

Я решил эту задачу. Площадь прямоугольного равностороннего треугольника [ABC] представляет собой движение. […Путь] AD будет пройден за время, представляемое [треугольником] ADE; а [путь] DB – за время, представляемое [трапецией] DEBC. Следует также отметить, что меньшая площадь [фигуры] представляет более медленное движение. [Площадь] AED составляет одну треть [площади] DEBC (Декарт полагал, что AD = DB. – И.Д.). Поэтому он [камень] пройдет [путь] AD в три раза медленнее, чем [путь] DB1484.

Рис. 3.4. К дневниковой записи Декарта по поводу задачи Бекмана (1618)

Нельзя сказать, что приведенная запись отличается ясностью формулировок (и это неудивительно, ведь Декарт делал ее для себя), но вместе с тем она вполне поддается трактовке и, на мой взгляд, совершенно однозначной. Запись эта означает, что расстояние AD камень пройдет со скоростью в три раза меньшей, чем расстояние DB. Если понимать выражение «пройти некий путь с некой скоростью V» в том смысле, что в конечной точке пути равноускоренно движущееся тело достигнет скорости V, то слова Декарта надо интерпретировать следующим образом: в точке D скорость камня будет в три раза меньше, чем в точке B, что, разумеется, неверно. (В действительности при условии AD = DB имеет место отношение V_D/V_B = 1/?–2.) Если же приведенное выражение трактовать как время, требующееся для преодоления данного расстояния (полагая, что чем больше телу требуется времени для преодоления одного и того же расстояния, тем меньше его скорость, то есть V₁/V₂ = T₂/T₁ при S₁ = S₂), то и тогда ответ Декарта неверен, ибо в действительности T_AD/T_DB = (?–2/(2 – ?–2)) при том же условии AD = DB.

Декарт же исходил из того, что «широта», то есть отрезок AB на рис. 3.4, представляет собой не время, как на рис. 3.2, но пройденный путь, тогда как площади фигур (треугольников и трапеций) на обоих рисунках представляют количество движения, накопленного телом к моменту прохождения им соответствующей части пути. Далее Декарт рассуждал так: площади фигур ADE и DEBC относятся как 1: 3. Следовательно, скорость, накопленная телом при прохождении отрезка DB, в три раза больше, чем скорость, накопленная при прохождении им равного по величине отрезка AD, то есть V_D/V_B = (площадь треугольника ADB): (площадь трапеции DEBC) = 1: 3, а значит T_AD/T_DB = 3: 1, так как V_D/V_B = T_DB/T_AD при S₁= AD = DB = S₂. Иными словами, вторую половину пути камень прошел в три раза быстрее первой. Видимо, Декарт полагал, что результат не изменится оттого, что вместо времени вертикальный отрезок станет представлять пройденный путь.

Сказанное выше свидетельствует о том, что в 1618 году у Декарта не было «ясного и отчетливого», как он любил выражаться, понимания природы равноускоренного движения и понятия скорости.

Следующее из дошедших до нас упоминаний Декартом задачи о свободном падении тел относится к 1629 году. Весной и летом этого года указанная задача обсуждалась в переписке Бекмана с Мареном Мерсенном [рис. 3.5]. Последний спустя некоторое время попросил Декарта высказать свои соображения по теме полемики. Декарт затронул проблему свободного падения в двух письмах Мерсенну – от 13 ноября и от 18 декабря 1629 года1485. Фактически Декарт повторил в них свои рассуждения, зафиксированные им в упомянутой дневникой записи 1618 года:

…Скорость движения в вакууме всегда возрастает в пропорции, о которой я упомянул выше и которую я нашел одиннадцать лет тому назад, когда передо мной была поставлена эта задача, и тогда же я записал решение в моем дневнике»1486.

Рис. 3.5. Филипп де Шампань (Ph. de Champaigne; 1602 – 1674). Портрет Марена Мерсенна

Здесь я позволю себе небольшое отступление. В тоне Декартова письма нетрудно уловить приоритетные обертоны. Это не случайно. Осенью 1629 года Мерсенн получил от Декарта некоторые вопросы и соображения, касавшиеся природы консонанса в музыке, и переслал их Бекману. Последний в ответном письме сообщил Мерсенну, что эти вопросы он (Бекман) впервые поставил перед Декартом еще во время их встреч в Бреде. Узнав (из письма Мерсенна) об этом заявлении своего друга, Декарт решил, что тот хочет представить себя его (Декарта) наставником в 1618 – 1619 годах. Мысль о том, что Бекман мог его чему-то научить, привела самолюбивого Декарта в негодование, и он на время прекратил с голландцем всякие отношения. Спустя год Мерсенн, будучи в гостях у Бекмана, с интересом ознакомился с его «рукописной книгой» (то есть с Journal), и последний не преминул вновь затронуть приоритетные вопросы. Узнав об этом, Декарт написал бывшему другу язвительное письмо, в котором заявил, что не слышал от него «ничего, кроме пустых фантазий», хотя, надо признать, «иногда случается, что, когда философские вопросы обсуждает даже совершенно не сведущий в них человек, он высказывает немало вещей, которые по чистой случайности совпадают с истиной»1487.

Неужели только… как бы это помягче сказать… аристократическая гордость помешала Декарту признать, что кто-то мог его учить? Разумеется, это обстоятельство сыграло свою роль, ибо «основатель философского и научного рационализма» (Н. Грот) скорее был склонен учить других, чем следовать чьим-либо наставлениям1488. Но была еще одна веская для Декарта причина столь негативно высказаться по поводу действительных или мнимых претензий Бекмана на интеллектуальное лидерство в их бредском тандеме. Декарт знал, что голландец собирается опубликовать свой трактат по физике, который должен был включать фрагменты из Journal. Если бы этот замысел оказался реализованным, то Декарту, который также планировал в конце 1620-х годов написать и издать пространное сочинение по физике, было бы очень трудно доказывать, какие идеи принадлежат ему, а какие Бекману. Французский мыслитель был не в восторге от того, что предлагавшиеся им объяснения природных явлений окажутся следствиями не интуитивно ясных первоначал мира, им же и сформулированных, но умозаключений некоего преподавателя из Дордрехта. Лучше уж быть обязанным Богу, конечному источнику наших интуитивно ясных понятий, нежели Бекману. Разумеется, воспрепятствовать публикации книги последнего1489 Декарт не мог, но он был в состоянии оказать психологическое давление на друга-соперника, возомнившего себя его учителем.

В действительности вопрос о том, насколько Декарт в интеллектуальном плане обязан Бекману, непрост. После того как в 1905 году голландский историк Корнелис де Ваард обнаружил и начиная с 1939 года стал публиковать Journal Бекмана, стало ясно, что дела обстояли, мягко говоря, не совсем так, как пытался их представить Декарт. Выяснилось, к примеру, что Бекман еще до знакомства с «Monsieur Ren? du Peron» разрабатывал «микромеханический» подход к объяснению природных явлений, сформулировал идею «сохранения движения» Богом, представление о «силе» движения, пропорциональной скорости и размерам тела; он также до и независимо от Декарта настаивал на необходимости устранения из физических объяснений всякого упоминания о каких-либо прирожденных телу причинах и т.д. Декарт действительно был многим обязан Бекману, и он это знал. Но вместе с тем многие важные идеи Декарт сформулировал самостоятельно и независимо от Бекмана. По мнению А. Койре, оригинальность Декарта как натурфилософа состоит прежде всего в том, что он решил основать новую физику «на “порядке разума”, а не на порядке материальных субстанций»1490. Однако, как признал Койре, в 1618 году Декарт «просто не воспользовался интеллектуальным сокровищем (prix) Бекмана»1491, оценив его лишь в свои зрелые (то есть 1640-е) годы1492.

Вернемся, однако, на главную колею нашего анализа картезианского решения задачи свободного падения тела. Детальное рассмотрение упомянутых выше писем Декарта Мерсенну (от 13 ноября и 18 декабря 1629 года)1493 говорит о том, что в это время французский философ придерживался в своей трактовке свободного падения того же мнения, что и в 1618 году. В этих письмах Декарт прямо указывает, что площади фигур (треугольников и трапеций) характеризуют скорости (celeritas) тела на соответствующих участках пути. Кроме того, вместо термина «сила [движения]», который в первоначальном документе обозначал «силу притяжения Земли» и «добавленную способность [движения]», накопленную телом по мере падения, Декарт теперь использует иные термины: «тяжесть» и «запечатленная сила» (или «импетус»). Все это лишний раз указывает на генетическую связь картезианского анализа движения с традицией «мертонских калькуляторов»1494, а также на недостаточность имевшихся в распоряжении Декарта математических средств для выражения функциональной зависимости одних величин от других.

Наконец, в первом из упомянутых выше писем Мерсенну Декарт формулирует полученные им ранее результаты в более общей форме:

…Если оно [тело] падает из точки A в точку B в течение трех моментов, то из точки B в точку C оно будет падать один момент (разумеется, при условии, что AB = BC [рис. 3.6]. – И.Д.). Таким образом, за четыре момента оно пройдет в два раза большее расстояние (то есть AC = 2AB. – И.Д.), чем то, которое оно прошло за три момента (AB), и, следовательно, за 12 моментов оно пройдет расстояние в два раза большее, чем за 9 моментов, а за 16 моментов в четыре раза большее, чем за 9, и т.д.1495

Здесь Декарт ошибся дважды. Во-первых, если разделить пройденный телом путь на четыре равные части, то при последовательном прохождении этих четырех отрезков скорости, достигаемые телом к концу каждого отрезка, как и площади соответствующих фигур, должны (если использовать подход Декарта) относиться друг к другу как 1: 3: 5: 7, а времена прохождения этих отрезков пути – как 1: 1/3: 1/5: 1/7. Таким образом, полное время должно быть равно 1 + 1/3 + 1/5 + 1/7 = 176/105, а потому время прохождения первого отрезка пути должно относиться ко времени прохождения всех четырех отрезков как 1: 176/105 = 105/176, что не равно отношению 9: 16. Но – и это во-вторых, – ни тот, ни другой результат не является правильным.

Рис. 3.6. К выводам Декарта о свободном падении тел, приведенным в письме Мерсенну от 13 ноября 1629 года

Позднее, в октябре 1631 года, Декарт признался Мерсенну, что возрастание скорости невозможно выразить рациональными числами1496. В принципе он был прав, потому что если к концу первого отрезка пути скорость оказывается равной величине v, то к концу второго отрезка (равного первому) она должна быть равна ?–3v, а к концу третьего – ?–3v и т.д. Однако в отличие от Галилея, который сумел найти корректное решение задачи много раньше, не позднее 1604 года, Декарт правильного решения так и не получил. Более того, он со временем уходил от него все дальше и дальше.

В октябре 1631 года Декарт пишет Мерсенну:

Что касается способа расчета скорости, о котором я Вам сообщал (речь идет о свободном падении. – И.Д.), то ему не следует придавать большого значения, поскольку он предполагает две вещи, которые наверняка являются ошибочными, а именно: что существует совершенно пустое пространство и что движение, которое происходит в нем в первый момент, то есть когда оно начинается, является самым медленным, какое только можно вообразить, и что затем оно постоянно равномерно возрастает1497.

Из этих строк видно, что Декарт, не ставя под сомнение чисто математическую сторону своего решения, усомнился в правильности использованных им физических допущений. Сомнительными ему представлялись два утверждения: существование пустоты и равноускоренный характер движения свободно падающего тела. По мнению Декарта, в ситуации реального падения тела сопротивление воздуха «всегда увеличивается в геометрической пропорции к скорости движения, и в конце концов движение достигает той точки, где оно уже не возрастает в заметной степени»1498. При этом он полагал, что скорость падающего в воздушной среде тела асимптотически стремится к некой предельной («особой, конечной») скорости. Кроме того, Декарт предположил, что тяжесть «не всегда действует одинаковым образом, подобно душе, но она [тяжесть] порождается неким другим телом, уже находящимся в движении»1499.

В конце 1632 года Декарт пишет Мерсенну:

…То, что Вы сообщили мне о расчете Галилеем скорости падающих тел, не имеет ничего общего с моей философией, которая утверждает, что два свинцовых шара [разного веса…] не будут падать с тем же самым отношением [скоростей], что два деревянных шара [имеющих те же веса…] Галилей не учел этих различий, и потому я подозреваю, что он не пришел к истине1500.

Вряд ли стоит специально останавливаться на ошибочности приведенных Декартом утверждений.

Иными словами, к началу 1630-х годов мысль Декарта пошла по скользкому пути определения причин движения тел под действием силы тяжести и природы самой тяжести. Но это я пишу отнюдь не в упрек французскому мыслителю. Каждому поколению ученых очень трудно (а чаще – невозможно) осознать, какие проблемы решаемы в данное время, а какие – нет. Искус искать причины, узнать суть и истинную «механику» явлений очень велик. И не каждый способен совершить подвиг конструктивного прагматизма, предполагающий трансляцию нашего естественного желания раскрыть причины исследуемого явления в интерьер познавательного процесса: «мы не знаем истинной природы тяготения (или естественного отбора, или электромагнитного поля, или периодичности свойств химических элементов и т.д.), но мы можем открыть закон, лежащий в основе данного явления».

Данный текст является ознакомительным фрагментом.